自动微分(Automatic Differentiation)

求任意函数的微分是数值方法中很重要的一个内容, 不同于计算物理中常用的简单数值微分, 这里我们介绍在ML等领域中常用的另一种微分方式: 自动微分
Author

Yuanqing Wu

Published

August 26, 2021

自动微分(Automatic Differentiation)

微分算法

对于几乎所有最优化方法来说, 最基础的一步就是求任意函数的微分. 例如梯度下降法(Gradient Descent). 因此, 微分算法的重要性自然不言而喻. 目前, 一共存在四种微分算法: * 手动微分(Manual Differentiation), 即手动求出函数的微分, 并直接编码进代码里. * 数值微分(Numerical Differentiation). 顾名思义, 求解任意函数在某一点的微分的数值解. * 符号微分(Symbolic Differentiation). 即Mathematica中提供的微分, 给出任意函数微分的解析表达式. * 自动微分(Automatic Differentiation).

其中手动微分由于每次修改模型, 我们都需要更改求解梯度的代码, 并且对于维度较高的函数编码量很大, 因此较少采用, 我们在此也不会涉及.

数值微分(Numerical Differentiation)

数值微分是最简单的一种计算微分的方法, 原理就是基于微分的定义: \[ f'(x) = \lim_{\epsilon \to 0} \frac{f(x+\epsilon) - f(x)}{\epsilon}\] 我们将\(\epsilon\) 取一个极小值(例如\(0.00001\)), 代入计算即可得到数值微分. 较为常用的是中心差分法: \[ f'(x) = \lim_{\epsilon \to 0} \frac{f(x+\epsilon) - f(x-\epsilon)}{2 \epsilon} \] 数值微分的优点是编码非常容易, 但缺点也很明显:第一, 计算量很大, 计算梯度时对于每个变量都需要计算两次函数值; 第二, 误差较大, 这一点在计算物理/数值方法课上应该都有过详细的讨论.

符号微分(Symbolic Differentiation)

符号微分即求得函数的微分的解析表达式. 其优点在于得到是精确解, 并且只需要求解一次表达式, 函数各点的微分都可以得到, 而缺点也很明显, 第一, 随着函数表达式复杂度的上升, 得到的微分解析式复杂度可能极速膨胀, 即所谓的”表达式膨胀”(expression swell)问题; 第二, 符号微分只能求解具有数学表达式形式的函数, 但很多时候我们使用的函数并不具有一个显式的表达式形式; 第三, 符号微分难以求解存在不可微点的函数.

自动微分(Automatic Differentiation)

终于到了今天的主角, 自动微分. 自动微分的想法其实可以看作手动微分和数值微分的结合: 由于绝大多数函数的微分都可以通过查表得到, 因此我们只需要实现对几个基本函数的手动微分, 之后利用链式法则, 每步都带入数值求解, 就能实现对于任意函数的精确微分了.
自动微分是目前综合性能最好的微分算法, 同时具有精确求解, 速度快, 可求解含有逻辑控制语句与部分不可微的函数等优点.

自动微分-Forward Mode

我们从一个例子开始讲解前向的自动微分算法.
考虑函数: \[ f(x_1, x_2) = \ln (x_1) + x_1 x_2 -\sin(x_2) \] 可以将其转化为如下的AST形式 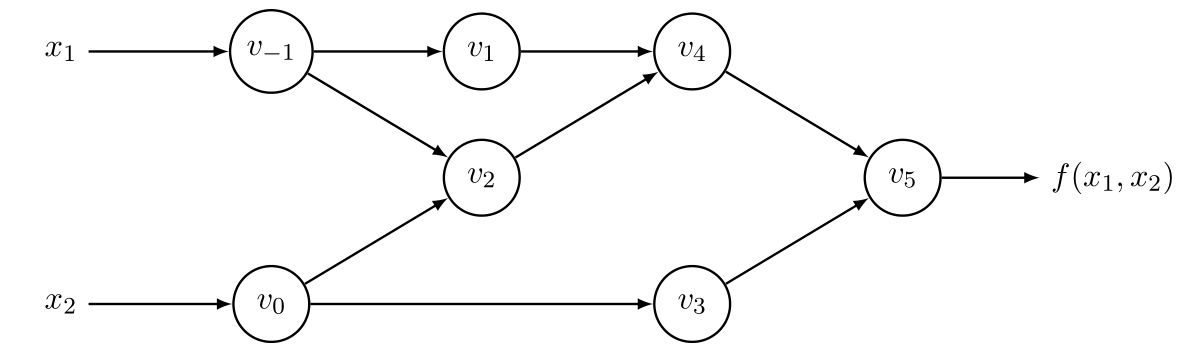2021-08-17-01-20-17 各节点分别为: * \(v_{-1}\) :\(x_1\) * \(v_0\) :\(x_2\) * \(v_1\) :\(\ln v_{-1}\) * \(v_2\) :\(v_{-1}\times v_0\) * \(v_3\) :\(\sin v_0\) * \(v_4\) :\(v_1 + v_2\) * \(v_5\) :\(v_4+v_3\)
之后, 就可以很轻松的求解函数在各步的函数值与导数值, 如下表所示. 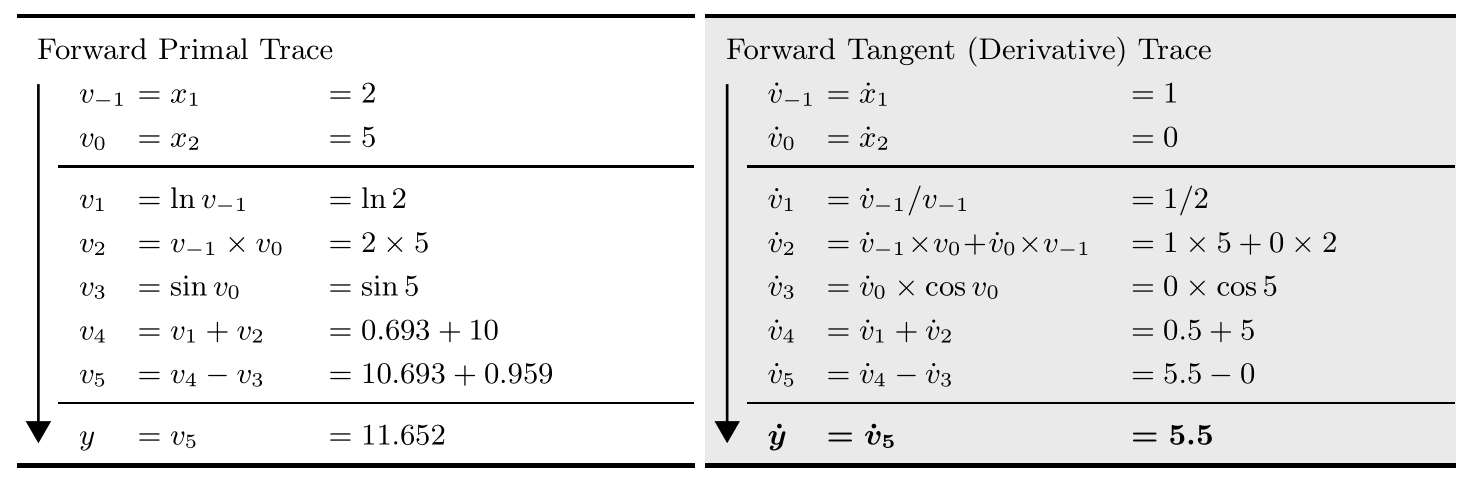2021-08-17-01-20-57 实现前向自动微分最简单的方法就是Dual Number法. 其核心思想是用\(x+\epsilon\)替换 \(x\)作为输入, 利用Taylor展开: \[ f(x+b \epsilon) = f(x) + f'(x)b \epsilon \] 例如, 我们需要求解\(\frac{\partial f}{\partial x_1}\), 则将\(v_{-1}\) 从\(x_1\)改为\(x_1 + \epsilon\). 之后, 我们需要实现各种基本函数下\(\epsilon\) 的作用率, 例如: * \((a+b \epsilon) + (c+ d \epsilon) = (a+c) + (b+d) \epsilon\) * \((a+b \epsilon)\times (c+d \epsilon) = ac + (bc+ ad)\epsilon\) * \(\ln (a+b \epsilon) = \ln a + \frac{b}{a}\epsilon\) * \(\sin (a+b \epsilon) = \sin(a)+ \cos (a) b \epsilon\)
之后, 依次计算各个节点: * \(v_{-1} = 2 + \epsilon\) * \(v_0 = 5\) * \(v_1 = \ln 2 + \frac{\epsilon}{2}\) * \(v_2 = 10 + 5 \epsilon\) * \(v_3 = \sin 5\) * \(v_4 = 10 + \ln 2 + \frac{11 \epsilon}{2} \approx 10.693 + 5.5 \epsilon\) * \(v_5 = 10.693 + \sin 5 + 5.5 \epsilon \approx 11.652 + 5.5 \epsilon\)

由此, 我们得到了在\((x_1=2, x_2=5)\)处, 函数值为\(10.693\), 对\(x_1\)的导数值为\(5.5\).
代码上的实现也是很简单的, 我们只要构造Dual Number类型:

struct DualNumber <: Number
    a::Float64;
    ϵ::Float64;
end

然后将各个基本函数重载(这里我们只重载了几个需要的函数):

# 重载运算符, 实现对DualNumber的运算
Base.:+(x::DualNumber, y::DualNumber) = DualNumber(x.a + y.a, x.ϵ + y.ϵ);
Base.:-(x::DualNumber, y::DualNumber) = DualNumber(x.a - y.a, x.ϵ - y.ϵ);
Base.:*(x::DualNumber, y::DualNumber) = DualNumber(x.a * y.a, x.ϵ * y.a + x.a * y.ϵ);
Base.log(x::DualNumber) = DualNumber(log(x.a), x.ϵ/x.a);
Base.sin(x::DualNumber) = DualNumber(sin(x.a), cos(x.a) * x.ϵ);
Base.tan(x::DualNumber) = DualNumber(tan(x.a), sec(x.a)^2*x.ϵ);
Base.sqrt(x::DualNumber) = DualNumber(sqrt(x.a), x.ϵ/(2*sqrt(x.a)));

实现前向自动微分的过程之后就相当简单了:

function FowardAD(f, v::Vector{Float64})::Vector{Float64}
    grad = Float64[]
    for i in 1:length(v)
        dualV = map(x->x==i ? DualNumber(v[x], 1) : DualNumber(v[x], 0), 1:length(v));
        push!(grad, f(dualV).ϵ)
    end
    grad
end
FowardAD (generic function with 1 method)

你很快就能发现我们这么做的优点:我们不需要对代码做任何更改, 我们可以接受并求解任何一个你能定义的函数. FowardAD函数接受一个任意的函数\(f\), 与一个\(n\)维的向量\([v_1, v_2,\cdots,v_{n}]\), 返回\(f\)在 \(v\)处的梯度 \([\partial f/\partial v_i]\).
下面是两个例子

g(x) = log(x[1]) + x[1]*x[2] - sin(x[2])
f(x) = sum(sin, x) + prod(tan, x) * sum(sqrt, x);
y = [2., 5.]
x = [0.986403, 0.140913, 0.294963, 0.837125, 0.650451];
println(FowardAD(f, x));
println(FowardAD(g, y));
[1.0135827245997349, 2.500134089883427, 1.7257370110780195, 1.1013890171195015, 1.2445004882356923]
[5.5, 1.7163378145367738]

可以看出, 对于\(f(x)\) 这种维数不定, 难以写出解析形式的函数, 代数微分难以求解, 但自动微分依然能得出相当精确的结果.

自动微分-Backward Mode

你可能会疑惑, 我们有了前向自动微分, 为什么还要研究什么Backward Mode自动微分呢? 答案很简单, 从前面的介绍你应当注意到, 对于一个\(n\) 维的函数, 如果我们想要求得它在某点的梯度, 那么我们需要进行\(n\) 次前向自动微分. 对于目前很多应用, 例如深度学习等, 函数的输入维数都是非常巨大的, 在这种情况下前向自动微分的效率就非常低, 这时就需要反向自动微分.
反向自动微分的原理也非常简单, 先进行一次正向的求解, 计算出每个节点处的函数值, 之后利用链式法则, 从后向前依次求出各节点的导数. 仍然用之前的例子: \[ f(x_1, x_2) = \ln x_1 + x_1\times x_2 - \sin x_2\] 2021-08-17-01-22-35 其中\(\overline{v_{i}}\) 指代\(\partial y/\partial v_{i}\). 需要注意的是, \(v_{i}\) 应该被保存, 以供后续使用.
反向自动微分的原理非常简单, 但是实现上较前向自动微分困难一些. Dual Number方法不能使用, 我们需要构造AST, 从而进行反向求解.
首先, 我们需要构造节点结构, 其中f标记函数类型, \(0\)为 \({\rm id}\), \(1\)为加, \(2\) 为减, \(3\) 为乘…
sons为子节点的列表, 长度取决于函数的参数个数.
value为该节点的函数值.
deri为该节点的导数值.
id为该节点的id, 主要用于区分输入.

mutable struct OpNode
    f::Int64;
    sons;
    value::Float64;
    deri::Float64
    id::Int64;
end

接下来, 实现了OpNode的默认构造函数, 导数默认置\(0\), 等待反向传播时再进行计算. id自动加一.

globalID = 0;
function OpNode(f, sons, value)
    global globalID;
    OpNode(f, sons, value, 0.0, globalID += 1);
end
OpNode

之后实现了对几种基本运算的重载:

function Base.:+(x::OpNode, y::OpNode)
    return OpNode(1, [x, y], x.value + y.value);
end

function Base.:-(x::OpNode, y::OpNode)
    return OpNode(2, [x, y], x.value - y.value);
end

function Base.:*(x::OpNode, y::OpNode)
    return OpNode(3, [x, y], x.value * y.value);
end

function Base.log(x::OpNode)
    return OpNode(4, [x], log(x.value));
end

function Base.sin(x::OpNode)
    return OpNode(5, [x], sin(x.value));
end

注意, 至此我们就可以在不修改函数代码的情况下构造出一个AST, 同时完成前向计算各节点的函数值.
现在, 我们可以来实现反向自动微分的核心代码了

function evaluate(root::OpNode)
    if root.f == 0
        return ;
    end
    if root.f == 1
        root.sons[1].deri += root.deri;
        root.sons[2].deri += root.deri;
        evaluate(root.sons[1]);
        evaluate(root.sons[2]);
        return ;
    end
    if root.f == 2
        root.sons[1].deri += root.deri;
        root.sons[2].deri -= root.deri;
        evaluate(root.sons[1]);
        evaluate(root.sons[2]);
        return ;
    end
    if root.f == 3
        root.sons[1].deri += root.deri*root.sons[2].value;
        root.sons[2].deri += root.deri*root.sons[1].value;
        evaluate(root.sons[1]);
        evaluate(root.sons[2]);
        return ;
    end
    if root.f == 4
        root.sons[1].deri += root.deri/root.sons[1].value;
        evaluate(root.sons[1]);
        return ;
    end
    if root.f == 5
        root.sons[1].deri += root.deri*cos(root.sons[1].value);
        evaluate(root.sons[1]);
        return ;
    end
end
evaluate (generic function with 1 method)

根据每个节点的函数种类, 我们应用链式法则求出其子节点的导数值. 之后递归调用求解其子节点, 直到sons为nothing,即抵达叶节点为止.
下面这个函数可以从计算完成的树中取出指定id的节点的导数值, 用于输出.

function getDeriByID(root::OpNode, id::Int64)
    if root.id == id
        return root.deri;
    end
    if root.sons === nothing
        return ;
    end
    for i in root.sons
        r = getDeriByID(i, id);
        if r!==nothing
            return r;
        end
    end
end
getDeriByID (generic function with 1 method)

之后, 我们就可以完成反向自动微分的完整逻辑了.

function BackwardAD(f, v::Vector{Float64})::Vector{Float64}
    res = zeros(length(v));
    root = f(map(x->OpNode(0, nothing, x), v));
    root.deri = 1.;
    evaluate(root);
    for i in 1:length(v)
        res[i] = getDeriByID(root, i);
    end
    return res;
end
BackwardAD (generic function with 1 method)

我们将输入向量v转变为一系列叶节点(即map(x->OpNode(0, nothing, x), v)语句), 并传入给定函数. 由于我们实现了对各基本操作的重载, 计算该函数时即完成了AST的构建和前向计算各节点函数值的过程, 并返回根节点. 之后, 将根节点的导数值设为1, 并开始反向自动微分. 完成后返回相应的梯度向量即可.
一个相同的例子:

f(x) = log(x[1]) + x[1]*x[2] - sin(x[2]);
println(BackwardAD(f, [2., 5.]));
[5.5, 1.7163378145367738]

Reference与Tips

  • 本文中所有图片来自于arXiv:1502.05767, 如果你想了解更多, 更严格的关于自动微分的内容, 强烈推荐你读一读这篇综述.
  • 本文中没有考虑多输出函数的情况. 实际上, 标准的Automatic Differentiation程序应当给出Jacobian矩阵, 而不是梯度向量. 相应的, 对于当输出维度很大, 而输入维度相对较小的情况下, 前向自动微分的性能就要优于反向自动微分了.
  • 关于两种自动微分, 本文中只展现了一个最简单, 最易实现的实现方式. 实际的自动微分有许多细节, 例如, 对AST进行图优化, 基于元编程的Differiatial Rule生成等等. 如果你想深入学习, 你应当读一读大项目中的AD实现. 作为推荐, Julia目前实现了一套相当好的可微分编程环境, 你可以读一读FowardDiff.jl以及ReverseDiff.jl的代码.